1.卡尔曼作用简述

卡尔曼滤波是一种递归的最优状态估计算法，用于传感器数据融合、导航系统和机器人 领域，核心思想，通过预测-更新循环，结合系统动态模型和当前测量值，对系统状态 做出最优估计。

2.卡尔曼核心步骤

2.1 预测步骤

状态预测 误差协方差预测

2.2 更新步骤

卡尔曼增益计算 状态更新 误差协方差更新

3.关键性参数

3.1 初始化状态估计X

系统初始状态的给定值（猜测），对于心率之类的，例如给定一个正常值。 若不准确，较大的初始化误差协方差，可使滤波器快速收敛。

3.2 初始误差协方差P

初始话状态估计的不确定性，值越大越不确定。 如果是初始化状态已经很明确，可以设置较小值，如果不确定则较大值

3.3 过程噪声协方差Q

系统动态模型的不确定性 Q较大，允许模型更快速适应变化，但是可能存在放大噪声 Q较小，强制轨迹平滑，有利于抑制噪声，但是可能滞后于真实值。

3.4 测量噪声协方差R

传感器测量误差的统计（例如：本文使用用gps轨迹，则和gps定位误差相关） 较大，降低对测量值的信任程度，更加依赖于预测值 较小，更信任测量值，滤波结果更加接近原始数据

3.5 状态转移矩阵F

描述系统状态如何随时间演变（如匀速运动、匀加速运动） 注意，必须要准确反应系统动态特性，否则滤波效果变差

4.调试指南

光凭参数，只需要了解参数控制内容，在熟悉各个参数获取 例如初始化状态获取，测量误差、对过滤结果预期是平滑还是反应真实做出 预判。比较重要是建立一个可以动态观察调试的平台。

5.实际效果

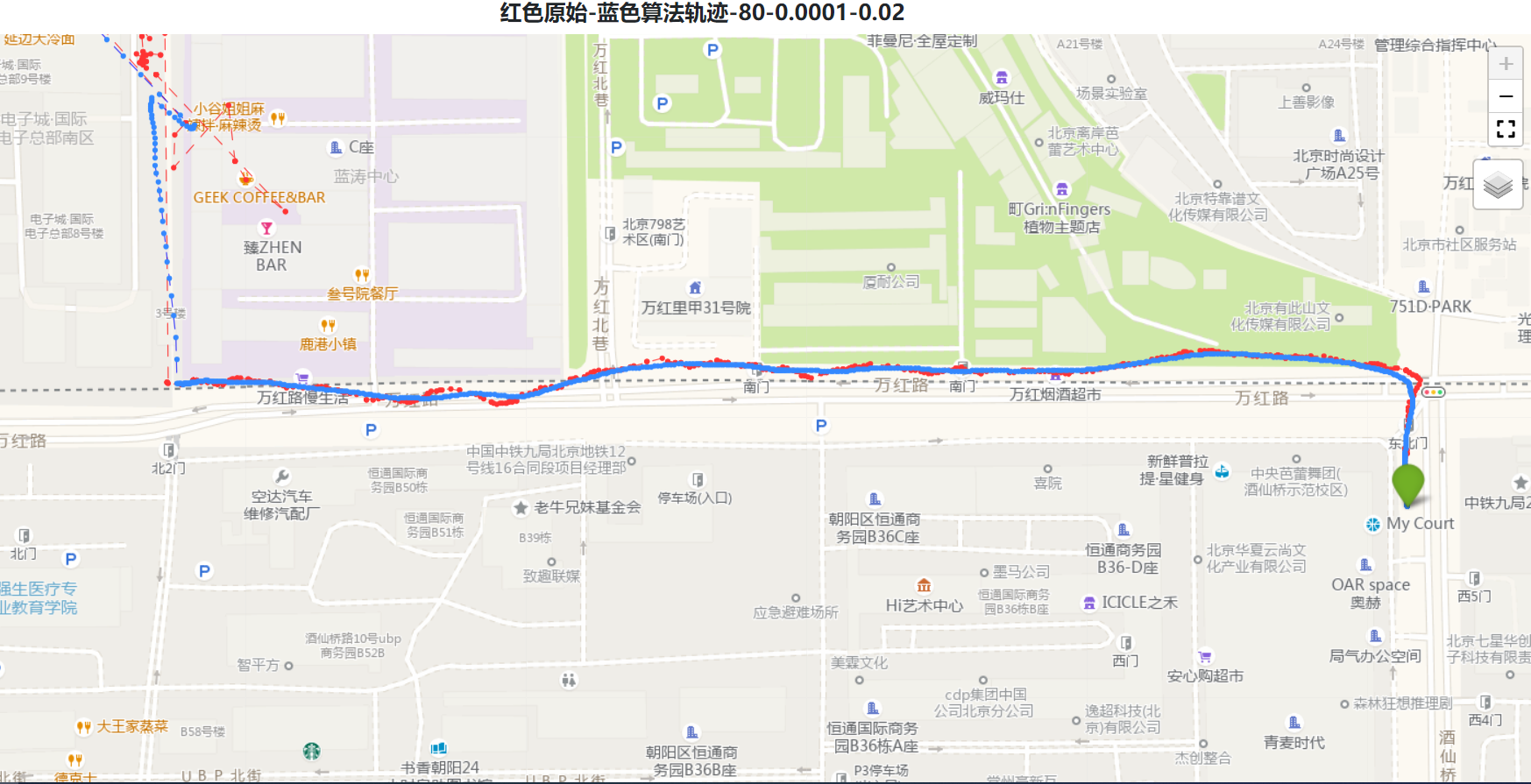
必须要建立一个可视化数据，这样才能方便于调试，各种参数的实际效果，如下，我们 以gps轨迹做一个扩展卡尔曼滤波效果评估（二维卡尔曼）。 通过python写一个可视化界面，直观看轨迹情况，方便进行分析。 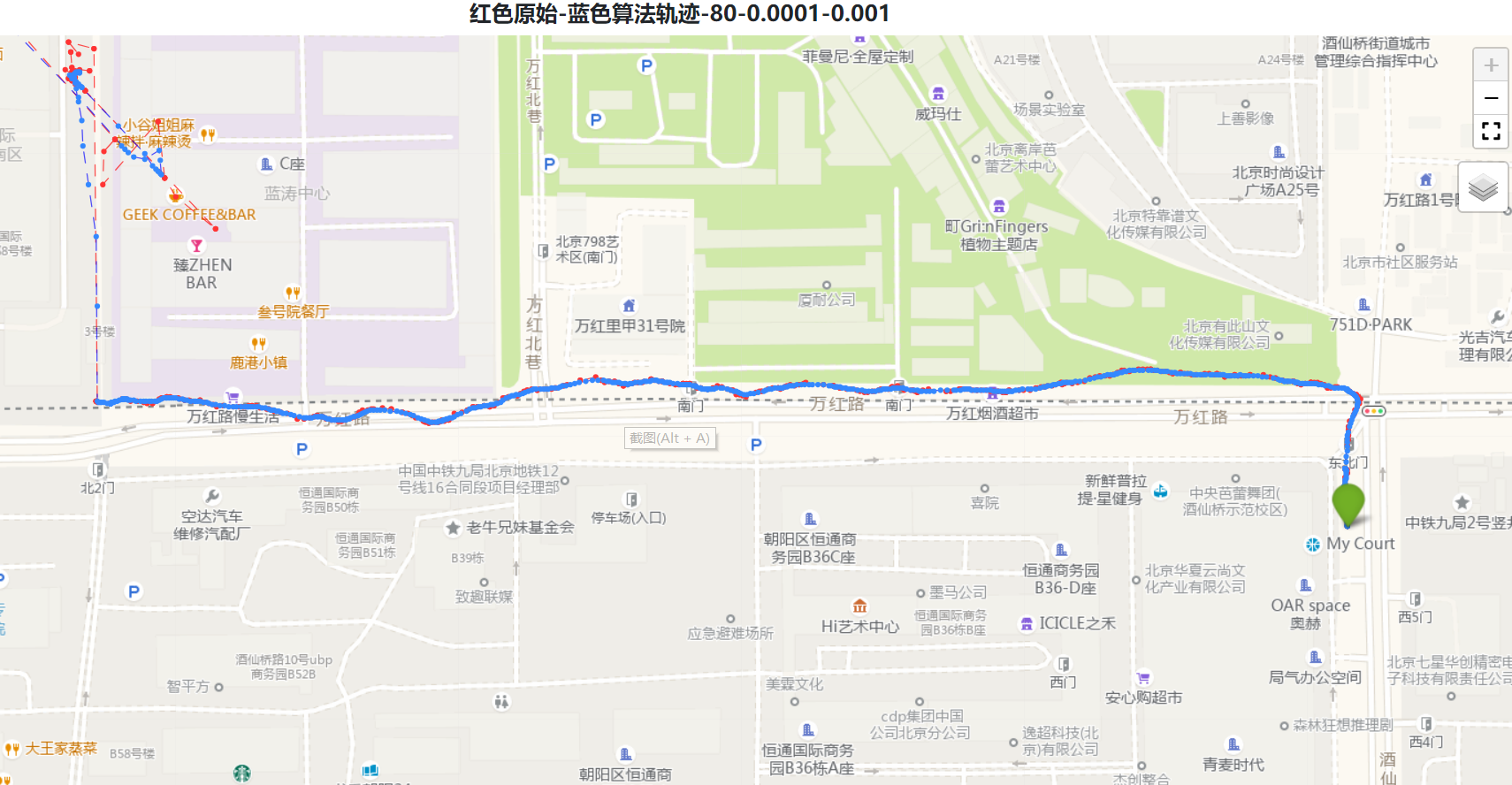从上面明显可以看到，选择越相信传感器，过滤倾向于原始（但是导致了gps部分漂移到 马路对面的轨迹），显然越相信传感器，轨迹不友好。